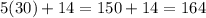Answer: B. 164
The value of y =30
The value of CD = 164
Explanation:
Properties of isosceles trapezoid:
- Two sides are parallel.
- The opposite non-parallel sides are equal.
- The diagonals are equal.
Given: ABCD is an isosceles trapezoid with diagonals that intersect at point P. AB || CD
⇒ BC= AD [opposite non-parallel sides]
AC=BD [ Diagonals are equal]
Since
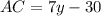 and
and
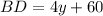
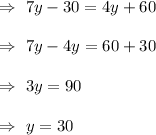
The value of CD =