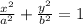A circle is defined, in loci form, as the distance from a single point being equidistant to a set of points (that is, the radius). Its distance is always constant and in general form follows: x² + y² = r².
An ellipse, in Layman's terms, is a special form of circle (but is not a circle, as circles are a strict set of rules), containing its own unique set of loci rules. An ellipse is the locus of points such that the distance from the foci to P, a fixed point is constant, and follows the general form: