Given the statement, "If
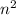
is odd, then

is odd," its contrapositive claims that, "If

is not odd, then
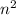
is not odd."
So assume

is not odd, i.e.

is even. This means there is an integer
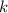
for which

. Squaring this gives
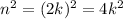
.
Well, we can write

, and
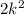
is just another integer, which means
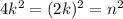
must be even.