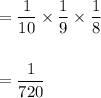Question

A train has 10 cars numbered 1 through 10. If the cars are coupled randomly, what is the probability that the first 3 cars are in car number order?

1/720

2/15

1/5,040

Answer 1

If they are in order the highest number for the first car is 7...and the other cars can only have one specific value because of the first, so

(7/10)(1/9)(1/8)=7/720

Okay, I see that they mean the order has to be 1,2,3 instead of all ordered sets like 7,8,9 and 4,5,6 for example...

So if they have to be 1,2,3 then

(1/10)(1/9)(1/8)=1/720

Answer 2

Hence, the probability that the first 3 cars are in car number order is:

`(1)/(720)`

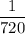
Explanation:

A train has 10 cars numbered 1 through 10.

If the cars are coupled randomly, what is the probability that the first 3 cars are in car number order.

The probability of the three cars is independent and we know that when the events A,B and C are independent then

`P(A\bigcap B\bigcap C)=P(A)* P(B)* P(C)`

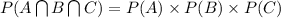
As, the first car chosen is to be selected among 10 cars.

Hence, the probability is:

`P(A)=(1)/(10)`

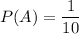
similarly the second car is to be selected among 9 cars.

Hence,

`P(B)=(1)/(9)`

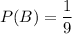
similarly,

`P(C)=(1)/(8)`

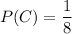
Hence, the probability that the first 3 cars are in car number order is:

`=(1)/(10)* (1)/(9)* (1)/(8)\\\\\\=(1)/(720)`