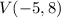Question

If we transform y = x2 by 5 units to the left and 8 units up, what is the vertex of the resulting parabola?

Answer 1

The vertex of the resulting parabola is (-5, 8).

Answer 2

`V(-5,8)`

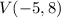
Explanation:

The given function is

`y=x^(2)`

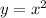
Notice that this is a parent function, that is, the simplest form of a quadratic function.

The transformations are:

1. 5 units to the left.
2. 8 units up.

Notice that this are rigid transformations, specifically, they are translations only.

Remeber, to move a function to the left, we must sum units to the x-variable. To move a function upwards, we must sum units to the y-variable.

Therefore, the transformed function is

`y=(x+5)^(2) +8`

Notice that the equation has the form
`y=a(x-h)^(2) +k`.

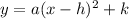Where
`a=1`,
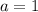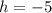`h=-5` and
`k=8`.

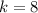Additionally, an important property of quadratic function is the vertex of the parabola which represents the function, which is at
`V(h,k).`

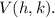
Therefore, in this case, the vertex is at
`V(-5,8)`