Question

Given the function h(x) = -22 – 5x + 13, determine the average rate of change

of the function over the interval -8 < x < 2.

Answer 1

Average rate of change = -5.6 for the function h(x) = -22 – 5x + 13, over the interval -8 < x < 2.

Explanation:

Given the function h(x) = -22 -5x + 13, determine the average rate of change

of the function over the interval -8 < x < 2.

The formula used to find average rate of change is:

`Average\:Rate\:of\:Change=(h(b)-h(a))/(b-a)`

We have a = -8 and b = 2

We need to find h(b) and h(a)

• Finding h(b):

Put x = 2 in the given equation: h(x) = -22 -5x + 13

h(2) = -22-5(2)+13

h(2) = -22-10+13

h(2) = -22-3

h(2) = -25

So, h(2) = -25

We get: h(b) =h(2) = -25

• Finding h(a):

Put x = -8 in the given equation: h(x) = -22 -5x + 13

h(-8) = -22-5(-8)+13

h(-8) = -22+40+13

h(-8) = 31

So, h(-8) = 31

We get: h(a) =h(-8) = 31

Putting values in formula and finding average rate of change.

`Average\:Rate\:of\:Change=(h(b)-h(a))/(b-a)\\Average\:Rate\:of\:Change=(h(2)-h(-8))/(2-(-8))\\Average\:Rate\:of\:Change=(-25-(31))/(2+8)\\Average\:Rate\:of\:Change=(-25-31)/(10)\\Average\:Rate\:of\:Change=(-56)/(10)\\Average\:Rate\:of\:Change=-5.6`

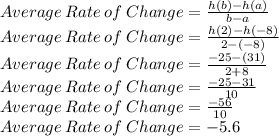
So, Average rate of change = -5.6 for the function h(x) = -22 – 5x + 13, over the interval -8 < x < 2.