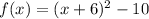Question

Given ​ f(x)=x^2+12x+26 ​. Enter the quadratic function in vertex form in the box.

Answer 1

Hello :
f(x)=x²+12x+26
= x² +2(6)(x) +36-36+26
= ( x² +2(6)(x) +6²) -10
=(x+6)²-10....... (vertex form )

Answer 2

The quadratic function in vertex form is
`f(x)=(x+6)^2-10`

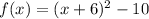
Explanation:

Given equation of quadratic function
`f(x)=x^2+12x+26`

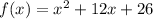
We have to write the given quadratic function in vertex form.

For a given quadratic function
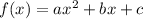`f(x)=ax^2+bx+c` can rewritten in standard form by completing the square.

The standard form of quadratic function
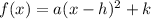`f(x)=a(x-h)^2+k` , where (h,k) denotes the vertex of the equation.

If a is positive, the graph opens upward, and if a is negative, then it opens downward.

Consider the given function
`f(x)=x^2+12x+26`

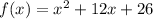
Using algebraic identity
`(a+b)^2=a^2+b^2+2ab`

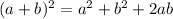
We have a = x and 2ab = 12x ⇒ b = 6

Adding
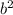`b^2` term to complete square and subtract so that the function remain same, we have,

`f(x)=x^2+12x+36-36+26`

`f(x)=(x+6)^2-10`

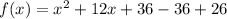
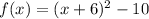
Which is in form of standard form of quadratic function.

Thus, The quadratic function in vertex form is
`f(x)=(x+6)^2-10`