Answer:
the base of the triangle is 8 cm
Explanation:
Area of a triangle(A) is given by:
 ....[1]
....[1]
where b is the base and h is the height of the triangle respectively.
As per the statement:
the height of a triangle is 7 cm longer than its base.
⇒
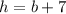
It is also given that: The area of the triangle is 60 cm²
⇒
 cm²
cm²
Substitute the given values in [1] we have;
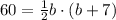
Multiply both sides by 2 we have;
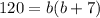
or
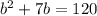
⇒
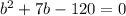
Now factorize this equations:
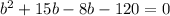
⇒
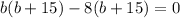
⇒
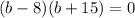
By zero product property we have;
b-8 = 0 and b+15 = 0
⇒b = 8 and b = -15
Since, the base of the triangle cannot be in negative.
⇒b = 8 cm
Therefore, the base of the triangle is 8 cm