Answer:
y = -⅔x + 2
Explanation:
Given the linear equation, 2(x-3) + 3y = 0, for which we must transform into its slope-intercept form, y = mx + b:
First, distribute 2 into the parenthesis:
2(x-3) + 3y = 0
2x - 6 + 3y = 0
Next, subtract both sides by 2x:
2x - 2x - 6 + 3y = - 2x
Then, add 6 to both sides of the equation:
- 6 + 6 + 3y = - 2x + 6
3y = -2x + 6
Lastly, divide both sides by 3 to isolate y:
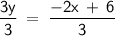
y = - ⅔x + 2 ⇒ This is the slope-intercept form.