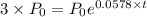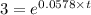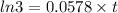Question

According to a survey, the population of a city doubled in 12 years. The annual rate of increase of the population of this city is approximately ____%. The population will grow to three times its current size in approximately ______ years.

2.50%; 5.78%; 12%; 50%

18 years; 19 years; 23 years; 24 years

Answer 1

You can find it by the original equation
2=(1+r)^12
r=(2)^(1÷12)−1
R=0.0595*100=5.95%

3=(1+0.0595)^t
t=log(3)÷log(1.0595)
t=19 years

Answer 2

5.78%

19 years

Explanation:

The Exponential Growth Model for a population has the next formula:

`P(t) = P_0 e^(k * t)`

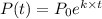
where P(t) is the population after t years,
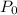`P_0` is the initial population, i. e., when t = 0, and k is the annual rate of increase of the population.

From data we know that the original population is doubled after 12 years. Replacing in the formula we get:

`2 * P_0 = P_0 e^(k * 12)`

`2 = e^(k * 12)`

`ln 2 = k * 12`

`k = (ln 2)/(12)`

`k = 0.0578`

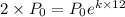
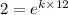
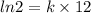
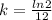
or 5.78 %

If the population grows to three times its current size, then:

`3 * P_0= P_0 e^(0.0578 * t)`

`3 =e^(0.0578 * t)`

`ln 3 = 0.0578 * t`

`t = (ln 3)/(0.0578)`

`t = 19`