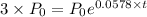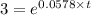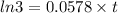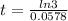Answer:
5.78%
19 years
Explanation:
The Exponential Growth Model for a population has the next formula:
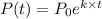
where P(t) is the population after t years,
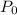 is the initial population, i. e., when t = 0, and k is the annual rate of increase of the population.
is the initial population, i. e., when t = 0, and k is the annual rate of increase of the population.
From data we know that the original population is doubled after 12 years. Replacing in the formula we get:
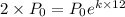
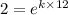
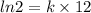
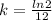
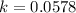
or 5.78 %
If the population grows to three times its current size, then: