Question

Consider the polynomial p(x)=16x^4-81y^4. Which of the following are equivalent expressions? Select all that apply

A: (4x^2-9y^2) (4x^2-9y^2)
B: (4x^2-9y^2) (4x^2+9y^2)
C: (4x^2+9y^2) (2x^3y) (2x-3y)
D: (4x^2+9y^2) (2x+3y) (2x+3y)
E: (4x^2+9y^2) (2x+3y) (2x-3y)

Answer 1

hello :
p(x)=16x^4-81y^4 = (4x²)²-(9y²)² = (4x²-9y²)(4x²+9y²)...(answer :B)

Answer 2

options (B) and (E) are correct.

`16x^2-81y^2=(4x^2+9y^2)(4x^2-9y^2)=(4x^2+9y^2)(2x-3y)(2x+3y)`

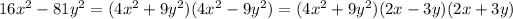
Explanation:

The given polynomial ,
`16x^4-81y^4`

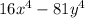
We have to choose an equivalent fraction from the given options,

Consider the given polynomial,

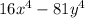`16x^4-81y^4` can be written as
`(4x^2)^2-(9y^2)^2`

Applying identity,
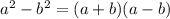`a^2-b^2=(a+b)(a-b)` , we get,

`(4x^2)^2-(9y^2)^2=(4x^2+9y^2)(4x^2-9y^2)`

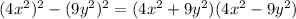
Again appplying the same identity on second bracket we get,

`(4x^2+9y^2)(4x^2-9y^2)=(4x^2+9y^2)((2x)^2-(3y)^2)`

Thus,
`(4x^2+9y^2)((2x)^2-(3y)^2)=(4x^2+9y^2)(2x-3y)(2x+3y)`

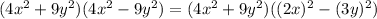
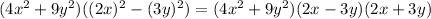
Thus, out of given options , options (B) and (E) are correct.