Answer:
1050
Explanation:
Lottery codes in the format XYZ
X is an uppercase vowel
Y is an uppercase consonant
Z can be any single-digit number
So, there are 5 vowels.
We need to select 1 vowel from these 5
There 21 consonants.
We need to select 1 consonant from these 21
There are 10 single digit number 9(including 0)
We need to select 1 single digit number from these 10
Now we will use combination to find how many lottery codes are possible
Formula :
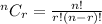
No. of lottery tickets are possible:
=
![^5C_1* ^(21)C_1 * ^(10)C_1/tex]</p><p> = [tex](5!)/(1!(5-1)!)*(21!)/(1!(21-1)!) *(10!)/(1!(10-1)!)](https://img.qammunity.org/2018/formulas/mathematics/high-school/6ja3b5ivu5ch01p72v5ebfb0cgf6zivph9.png)
=
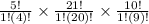
=
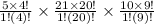
=
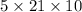
=
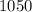
Hence 1050 lottery tickets are possible.