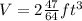Answer:
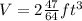
Explanation:
The volume of a rectangular prism is defined as

Where
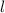 is length,
is length,
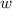 is width and
is width and
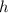 is height.
is height.
In this case, the dimensions are
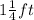 ,
,
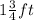 and
and
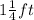 .
.
First, we need to transform all mixed numbers into fractions.
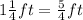
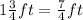
So, using the formula
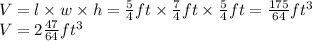
Therefore, the volume of the suitcase is