First, examine what happens over the integration domain.
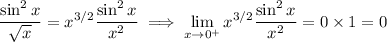
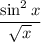
is continuous for
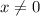
, so we don't need to worry about the right endpoint.
Now, note that
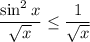
due to the fact that
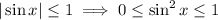
. So, if the larger integral converges, so must the smaller one. You have
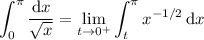
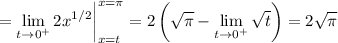
so the larger integral converges. Therefore the smaller one does, too.