Question

Your friend, a world-class long jumper, is trapped on the roof of a burning building. His only escape route is to jump to the roof of the next building. Fortunately for him, he is in telephone contact with you, a Physics 131 student, for advice on how to proceed. He has two options. He can jump to the next building by using the long-jump technique where he jumps at 45o to the horizontal. Or, he can take his chances by staying where he is in the hopes that the fire department will rescue him. You learn from the building engineers that the next building is 10 m away horizontally and the roof is 3 m below the roof of the burning building. You also know that his best long-jump distance is 7.9 m . What do you advise him to do

Answer 1

y = 7.33 m, x= 3 m, t = 1.608 s

it is still higher than the second building, which indicates that if it jumps it will be saved

Step-by-step explanation:

Let's use the projectile launch ratios, let's start with the range ratio

R = v₀² sin² 2θ / g

in this case the range is R = 7.9m and the angle is 45º, let's find the initial velocity

v₀² = R g / sin² 2θ

let's calculate

v₀ =
`\sqrt{ ( 7.9 \ 9.8)/( 1) }`

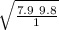
v₀ = 8.80 m / s

Let's find the components of the initial velocity

v₀ₓ = v₀ cos 45 = 8.80 cos 45

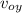`v_(oy)` = v₀ sin 45 = 8.80 sin 45

v₀ₓ = 6.22 m / s

v_{oy} = 6.22 m / s

To save yourself, you have to be at the same time as the other building or higher.

x = v₀ₓ t

t = x / v₀ₓ

t = 10 / 6.22

t = 1.608 s

let's see how much it has descended in this time

y =y₀ + v_{oy} t - ½ g t²

y = 10+ 6.22 1.608 - ½ 9.8 1.608²

y = 7.33 m

therefore it is still higher than the second building, which indicates that if it jumps it will be saved