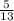Question

can someone help me with this?  Given 

sinx=0.9  , what is  cosx  ?

Answer 1

Question 1)
Given that sin(x) = 0.9, we can deduce that sin(x) =
`(0.9)/(1)`
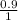
We can set up a triangle with angle
`x` and the opposite side as 0.9 and hypotenuse as 1.

Now, we know by pythagoras that hypotenuse² = side 1² + side 2²
So, to get side 2, we can take the square root of hypotenuse² - side 1² (ie
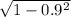
`\sqrt{1 - 0.9^(2)}` = 0.435889894...

Taking cosx will give us:

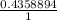
`(0.4358894)/(1)` = 0.4358894...

Question (2)
Given that cosA =
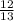
`(12)/(13)`, find sinA

Well, we can draw up a triangle, with hypotenuse 13, and adjacent side 12.
This is a pythagorean triad and you should recognise it in the future. The missing opposite side is 5, as 169 -144 = 25.

Now, you can find what sinA is (opposite/adjacent):

`(5)/(13)`

Answer 2

We are told that the sine (x) = 0.9 meaning that the sine of angle "x" equals 0.9.
To find the degrees of that angle, we look up the arc sine of 0.9 which equals
64.158 Degrees
So, now we look up the cosine of 64.158 degrees which is 0.43589 and that is what we had to find out.
*****************************************************
Well, if the answer needs to be in a fraction, let's try another approach.
If sine (x) = .9 that means that the opposite side/ hypotenuse = .9 / 1
and that means (by Pythagorean Theorem) the adjacent side^2 = hypotenuse^2 - .9^2
adjacent^2 = 1 -.81
adjacent^2 = .19
so adjacent side = square root of .19
and so the cosine of x = square root of .19 / 1