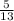Question 1)
Given that sin(x) = 0.9, we can deduce that sin(x) =
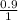
We can set up a triangle with angle

and the opposite side as 0.9 and hypotenuse as 1.
Now, we know by pythagoras that hypotenuse² = side 1² + side 2²
So, to get side 2, we can take the square root of hypotenuse² - side 1² (ie
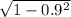
= 0.435889894...
Taking cosx will give us:
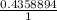
= 0.4358894...
Question (2)
Given that cosA =
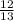
, find sinA
Well, we can draw up a triangle, with hypotenuse 13, and adjacent side 12.
This is a pythagorean triad and you should recognise it in the future. The missing opposite side is 5, as 169 -144 = 25.
Now, you can find what sinA is (opposite/adjacent):