A decimal expansion of a rational number either terminates or follows a repeating pattern of a *finite* sequence of digits.
Neither of these is the case here. The decimal expansion is obviously non-terminating, nor is the sequence of digits finite.
Writing the number as
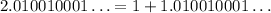
and only considering the second number, you have the following sequence of digits:
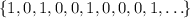
, where the

th term, starting with
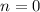
corresponds to the number

. The sequence can be described recursively by the recurrence
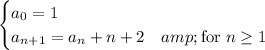
and explicitly by
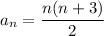
.
This sequence is not periodic, and indeed diverges to
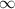
as
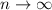
. This means the number cannot be rational.