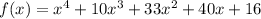Answer:
The quartic function is:
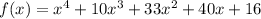
Explanation:
Quartic function--
A quartic function is a polynomial function with degree 4.
Now we know that for any quartic funtcion with just two roots "a" and "b" the equation of the function is calculated as:
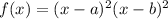
Here let a= -4 and b= -1
Hence, the equation of a quartic function is calculated as follows:
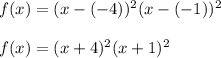
Now as we know that:
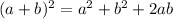
Hence,
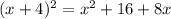
and
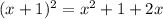
Hence,
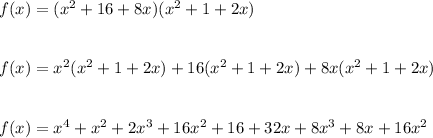
on combining like terms we have: