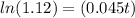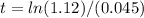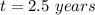Question

Your bank account is sitting on $14,000. You started with a principal balance of $12,500. If the interest rate was 4.5% compounded continuously, how long was your money in the bank?

Answer 1

`t=2.5\ years`

Explanation:

we know that

The formula to calculate continuously compounded interest is equal to

`A=P(e)^(rt)`

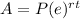
where

A is the Final Investment Value

P is the Principal amount of money to be invested

r is the rate of interest in decimal

t is Number of Time Periods

e is the mathematical constant number

we have

`t=?\ years\\ P=\$12,500\\P=\$14,000\\ r=4.5\%=4.5/100=0.045`

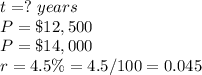
substitute in the formula above and solve for t

`14,000=12,500(e)^(0.045t)`

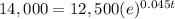
Simplify

`14,000/12,500=(e)^(0.045t)`

`1.12=(e)^(0.045t)`

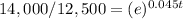
Apply ln both sides

`ln(1.12)=ln[(e)^(0.045t)]`

`ln(1.12)=(0.045t)ln(e)`

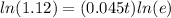
Remember that

`ln(e)=1`

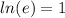
so

`ln(1.12)=(0.045t)`

`t=ln(1.12)/(0.045)`

`t=2.5\ years`