Question

Particle A of charge 2.76 10-4 C is at the origin, particle B of charge -6.54 10-4 C is at (4.00 m, 0), and particle C of charge 1.02 10-4 C is at (0, 3.00 m). We wish to find the net electric force on C. What is the x component of the electric force?

Answer 1

a) F_net = 30.47 N , θ = 10.6º

b) Fₓ = 29.95 N

Step-by-step explanation:

For this exercise we use coulomb's law

F₁₂ = k
`k ( q_(1) \ q_(2) )/( r^(2) )`

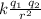
the direction of the force is on the line between the two charges and the sense is repulsive if the charges are equal and attractive if the charges are different.

As we have several charges, the easiest way to solve the problem is to add the components of the force in each axis, see attached for a diagram of the forces

X axis

Fₓ =
`F_(bc x)`

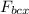
Y axis

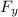`F_(y)`Fy =
`F_(ab) - F_(bc y)`

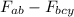
let's find the magnitude of each force

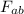`F_(ab)` = 9 10⁹ 2.76 10⁻⁴ 1.02 10⁻⁴ / 3²

F_{ab} = 2.82 10¹ N

F_{ab} = 28.2 N

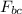`F_(bc)` = 9 10⁹ 6.54 10⁻⁴ 1.02 10⁻⁴ / 4²

F_{bc} = 3.75 10¹ N

F_{bc} = 37.5 N

let's use trigonometry to decompose this force

tan θ = y / x

θ = tan⁻¹ and x

θ= tan⁻¹ ¾

θ = 37º

let's break down the force

sin 37 = F_{bcy} / F_{bc}

F_{bcy} = F_{bc} sin 37

F_{bcy} = 37.5 sin 37

F_{bcy} = 22.57 N

cos 37 = F_{bcx} /F_{bc}

F_{bcx} = F_{bc} cos 37

F_{bcx} = 37.5 cos 37

F_{bcx} = 29.95 N

let's do the sum to find the net force

X axis

Fₓ = 29.95 N

Axis y

Fy = 28.2 -22.57

Fy = 5.63 N

we can give the result in two ways

a) F_net = Fₓ i ^ +
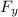`F_(y)` j ^

F_net = 29.95 i ^ + 5.63 j ^

b) in the form of module and angle

let's use the Pythagorean theorem

F_net =
`\sqrt{ F_(x)^2 + F_(y)^2 }`

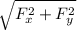
F_net = √(29.95² + 5.63²)

F_net = 30.47 N

we use trigonometry for the direction

tan θ=
`( F_(y) )/( F_(x) )`

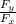
θ = tan⁻¹ \frac{ F_{y} }{ F_{x} }

θ = tan⁻¹ (5.63 / 29.95)

θ = 10.6º