Answer:
a) F_net = 30.47 N , θ = 10.6º
b) Fₓ = 29.95 N
Step-by-step explanation:
For this exercise we use coulomb's law
F₁₂ = k
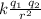
the direction of the force is on the line between the two charges and the sense is repulsive if the charges are equal and attractive if the charges are different.
As we have several charges, the easiest way to solve the problem is to add the components of the force in each axis, see attached for a diagram of the forces
X axis
Fₓ =
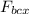
Y axis
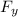 Fy =
Fy =

let's find the magnitude of each force
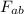 = 9 10⁹ 2.76 10⁻⁴ 1.02 10⁻⁴ / 3²
= 9 10⁹ 2.76 10⁻⁴ 1.02 10⁻⁴ / 3²
F_{ab} = 2.82 10¹ N
F_{ab} = 28.2 N
 = 9 10⁹ 6.54 10⁻⁴ 1.02 10⁻⁴ / 4²
= 9 10⁹ 6.54 10⁻⁴ 1.02 10⁻⁴ / 4²
F_{bc} = 3.75 10¹ N
F_{bc} = 37.5 N
let's use trigonometry to decompose this force
tan θ = y / x
θ = tan⁻¹ and x
θ= tan⁻¹ ¾
θ = 37º
let's break down the force
sin 37 = F_{bcy} / F_{bc}
F_{bcy} = F_{bc} sin 37
F_{bcy} = 37.5 sin 37
F_{bcy} = 22.57 N
cos 37 = F_{bcx} /F_{bc}
F_{bcx} = F_{bc} cos 37
F_{bcx} = 37.5 cos 37
F_{bcx} = 29.95 N
let's do the sum to find the net force
X axis
Fₓ = 29.95 N
Axis y
Fy = 28.2 -22.57
Fy = 5.63 N
we can give the result in two ways
a) F_net = Fₓ i ^ +
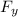 j ^
j ^
F_net = 29.95 i ^ + 5.63 j ^
b) in the form of module and angle
let's use the Pythagorean theorem
F_net =
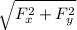
F_net = √(29.95² + 5.63²)
F_net = 30.47 N
we use trigonometry for the direction
tan θ=
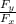
θ = tan⁻¹ \frac{ F_{y} }{ F_{x} }
θ = tan⁻¹ (5.63 / 29.95)
θ = 10.6º