Question

A horizontal curve of a two-lane undivided highway (12-foot lanes) has a radius of 678 feet to the center line of the roadway. An old building (sight obstruction) is located 30 feet from the edge of the innermost lane. The road is level and the superelevation is 0.06. Please determine the maximum speed for safe vehicle operation on this horizontal curve.

Answer 1

maximum speed for safe vehicle operation = 55mph

Step-by-step explanation:

Given data :

radius ( R ) = 678 ft

old building located ( m )= 30 ft

super elevation = 0.06

Determine the maximum speed for safe vehicle operation

firstly calculate the stopping sight distance

m = R ( 1 - cos
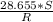`(28.655*S)/(R)` ) ---- ( 1 )

R = 678

m ( horizontal sightline ) = 30 ft

back to equation 1

30 = 678 ( 1 - cos (28.655 *s / 678 ) )

( 1 - cos (28.655 *s / 678 ) ) = 30 / 678 = 0.044

cos
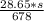`(28.65 *s )/(678)` = 1.044

hence ; 28.65 * s = 678 * 0.2956

s = 6.99 ≈ 7 ft

next we will calculate the design speed ( u ) using the formula below

S = 1.47 ut +
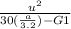`(u^2)/(30((a)/(3.2) )-G1)` ---- ( 2 )

t = reaction time, a = vehicle acceleration, G1 = grade percentage

assuming ; t = 2.5 sec , a = 11.2 ft/sec^2, G1 = 0

back to equation 2

6.99 = 1.47 * u * 2.5 +
`(u^2)/(30[(11.2/32.2)-0 ])`

3.675 u + 0.0958 u^2 - 6.99 = 0

u ( 3.675 + 0.0958 u ) = 6.99