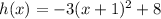ANSWER
The correct answer is
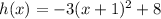
Step-by-step explanation
The function we want to write in vertex form is
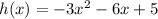
We factor -3 out of the first two terms to obtain,

We add and subtract half the coefficient of

multiplied by a factor of
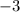
to get;
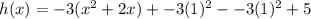
The expression becomes
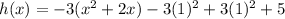
We factor -3 again out of the first two terms to get,
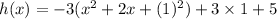
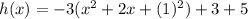
The expression in the parenthesis now becomes a perfect square.
This implies that;