Question

With water from one hose, a swimming pool can be filled in 8 hours. A second, larger hose used alone can gill the pool in 6 hours. How long would it take to fill the pool if both hoses were used simultaneously?

Answer 1

so. the smaller hose, can fill the pool in 8hrs
in 1hr then, it really has done only 1/8 of the job

if we take the filled pool to be the total job time, or "t"
then the smaller hose in 1hr has only done only 1/8 in "t" amount or
`\bf \cfrac{1}{8}t`

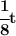
now, the bigger hose, can do the filling in 6hrs
that means in 1hr, it has only done then 1/6 in "t" time or
`\cfrac{1}{6}t`

now, the whole job, is a whole, or 1

so.. let us add those rates of each hose together, to see how long they'd take
`\bf \cfrac{1}{8}t+\cfrac{1}{6}t=1\implies \cfrac{t}{8}+\cfrac{t}{6}=1`

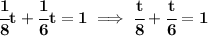
solve for "t"