Question

Scarlett is trying to find the height of a dam. She stands 90 meters away from the dam and records the angle of elevation to the top of the dam to be 26º.

Scarlett's height is 1.65 meters, so the height of the dam is () meters.

Answer 1

The height of the dam is 45.54 m.

Explanation:

Given : Scarlett is trying to find the height of a dam. She stands 90 meters away from the dam and records the angle of elevation to the top of the dam to be 26º. Scarlett's height is 1.65 meters.

To find : The height of the dam ?

Solution :

Refer the attached figure to clear the image of question.

The Scarlett's height be EC= 1.65 meters

She stands 90 meters away from the dam i.e. DE = BC = 90 m

The angle of elevation to the top of the dam to be 26º i.e. ∠BCA = 26°

Now,

Height of the Dam is AD = BD+AB

As, BD = EC = 1.65

We apply trigonometry, In ΔABC

`\tan \theta = \frac{\text{Perpendicular}}{\text{Base}}`

`\tan26^(\circ) = (DE)/(BE)`

`\tan26^(\circ) =(DE)/(90)`

`0.48773 * 90=DE`

`DE=43.89`

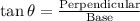
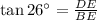
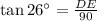
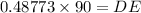
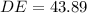
Substitute the value,

Height of the Dam is AD=1.65+43.89=45.54 m

Therefore, the height of the dam is 45.54 m.

Answer 2

45.54m

Explanation:

Refer the attached figure

Scarlett's height = AB = 1.65 meters

She stands 90 meters away from the dam i.e. BE = AC = 90 m

She records the angle of elevation to the top of the dam to be 26º i.e. ∠DBE = 26°

Height of the Dam = DC = EC+DE

AB = EC = 1.65

In ΔBDE

`Tan \theta = (Perpendicular)/(Base)`

`Tan 26^(\circ) = (DE)/(BE)`

`Tan 26^(\circ) = (DE)/(90)`

`0.48773 * 90=DE`

`43.89=DE`

Height of the Dam = DC =1.65+43.89=45.54 m

Hence the height of the dam is 45.54 m.