Answer:
The equation of parabola is given by:
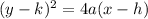
where,
(h, k) is the vertex.
Focus = (h+a, k)
As per the statement:
A parabola has a vertex at (0,0).
⇒
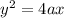
The focus of the parabola is located at (4,0).
⇒
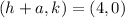
⇒
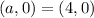
⇒a = 4
then, equation become:
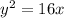
We have to find the equation of directrix
The equation of directrix is, x = h-a
then;
x = 0-4 = -4
⇒x = -4
Therefore, the equation of directrix is, x = -4