Answer:

Explanation:

To get vertex form of equation y =a(x-h)^2+k
we use completing the square method
In completing the square method we take coefficient of x ,divide by 2 and then we square it
To apply completing the square method, we make x^2 alone
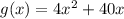
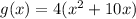
Coefficient of x is 10 , 10 divide by 2= 5
5^2= 25
Add and subtract 25
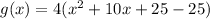
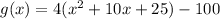
Now factor x^2 +10x+25, it becomes
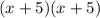
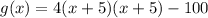
 is our vertex form
is our vertex form