Answer:
The speed of the river's current is 4.5 km/hr.
Explanation:
Given : A fisherman traveled in a boat from point N upstream.
After having traveled 6 km, he stopped rowing and 2 hour 40 min after first leaving N, he was brought back to N by the current.
Knowing that the speed of the boat in still water is 9 km/hour
To find : The speed of the river’s current.
Solution :
Let the speed of current = x km/h
Speed of boat = 9 km/h
Thus, the speed in upstream = (9 - x) km/h
Also, the speed in downstream = x km/h (because the boat is stationary in downstream)
Total distance = 6 km ( from N to the point he reached )
Total time = 2 hours 40 minutes
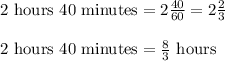
We know,
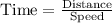
According to the question,
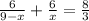
Taking LCM and 6 common
![6[(x+9-x)/((9-x)x)]=(8)/(3)](https://img.qammunity.org/2018/formulas/mathematics/high-school/mnkpl6osivrdctkl2o0zpu2cfuk6n0v23p.png)
Take 6 to another side,

Cross multiply,
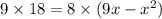
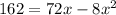
Taking 4 common and cancel out
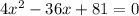
Solve quadratic equation by middle term split,


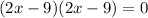
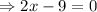
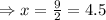
Therefore, The speed of the river's current is 4.5 km/hr.