Question

A fisherman traveled in a boat from point N upstream. After having traveled 6 km, he stopped rowing and 2 hour 40 min after first leaving N, he was brought back to N by the current. Knowing that the speed of the boat in still water is 9 km/hour, find the speed of the river’s current.

Answer 1

The speed of the river's current is 4.5 km/hr.

Explanation:

Given : A fisherman traveled in a boat from point N upstream.

After having traveled 6 km, he stopped rowing and 2 hour 40 min after first leaving N, he was brought back to N by the current.

Knowing that the speed of the boat in still water is 9 km/hour

To find : The speed of the river’s current.

Solution :

Let the speed of current = x km/h

Speed of boat = 9 km/h

Thus, the speed in upstream = (9 - x) km/h

Also, the speed in downstream = x km/h (because the boat is stationary in downstream)

Total distance = 6 km ( from N to the point he reached )

Total time = 2 hours 40 minutes

`\text{2 hours 40 minutes}=2(40)/(60)=2 (2)/(3) \\\\\text{2 hours 40 minutes}=(8)/(3) \text{ hours}`

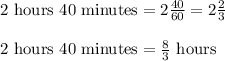
We know,
`\text{Time} = \frac{\text{Distance}}{\text{Speed}}`

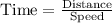
According to the question,

`(6)/(9-x)+(6)/(x)=(8)/(3)`

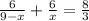
Taking LCM and 6 common

`6[(x+9-x)/((9-x)x)]=(8)/(3)`

Take 6 to another side,

`(9)/(9x-x^2)=(8)/(3* 6)`

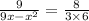
Cross multiply,

`9* 18=8*(9x-x^2)`

`162=72x-8x^2`

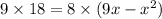
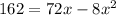
Taking 4 common and cancel out

`4x^2-36x+81=0`

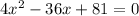
Solve quadratic equation by middle term split,

`4x^2-18x-18x+81=0`

`2x(2x-9)-9(2x-9)=0`

`(2x-9)(2x-9)=0`

`\Rightarrow 2x-9=0`

`\Rightarrow x=(9)/(2)=4.5`

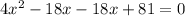
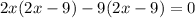
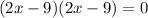
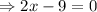
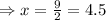
Therefore, The speed of the river's current is 4.5 km/hr.