Answer:
15
Explanation:
The given function is
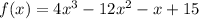
We need to find the y-coordinate of the y-intercept for the given function.
Substitute x=0 in the given function to find the y-intercept of the function.
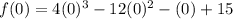
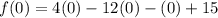
On further simplification we get
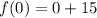
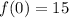
The function intersect y-axis at (0,15).
x-coordinate of the y-intercept = 0
y-coordinate of the y-intercept = 15
Therefore the y-coordinate of the y-intercept for the given function is 15.