Answer:
Since, the exponential decay function that models the present value,
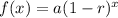
Where, a shows the initial value,
r shows rate of decay per period,
x is the number of periods,
Given,
Annual rate = 8 % = 0.08
1. 1 year = 12 months
So, monthly rate, r =

Number of periods in x years, t = 12x
Thus, the function would be,
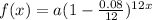
2. 1 year = 52 weeks
So, weekly rate, r =
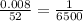
Number of periods in x years, t = 52x
Thus, the function would be,
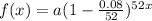
3. 1 year = 365 days
So, daily rate, r =
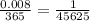
Number of periods in x years, t = 365x
Thus, the function would be,

4. Since, with increasing time the value of car will decrease,
Hence, there is an inverse relation between the amount of decrease and the time interval measured.