Answer:
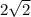 or 2.828
or 2.828
Explanation:
The given equation is

Let the mean distance from the sun of planet X is A then
mean distance from the sun of planet Y is 2A.
Therefore, we have
For planet X-
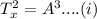
For planet Y-
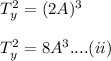
Divide equation (i) and (ii)
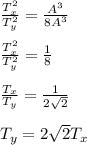
Therefore, we can conclude that orbital period is increase by a factor of
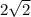 or 2.828
or 2.828