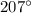we know that
The inscribed angle measures half that of the arc comprising
in this problem
m∠DGF -----> is a inscribed angle
m∠DGF=
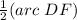
we have
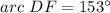
substitute
m∠DGF=
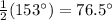
we know that
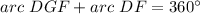
Find the measure of arc DGF
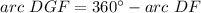
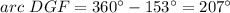
therefore
the answer is
a) the measure of inscribed angle m∠DGF is
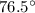
b) the measure of arc DGF is