Answer:
Please check the explanation.
Explanation:
Given the system of equations
2 + 2y = 6
2x - 3y = 26
Let us solve the system of equations

Rearrange equations
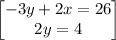
Multiply -3y+2x=26 by 2: -6y+4x=52
Multiply 2y = 4 by 3: 6y = 12

adding the equations
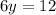

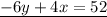

Solve 4x = 64 for x
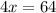
divide both sides by 4

Simplify
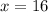
For -6y+4x = 52 plug in x = 16

Multiply the numbers: 4 · 16 = 64

Subtract 64 from both sides

Simplify

Divide both sides by -6

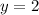
Therefore, the solution to the system of equations be:
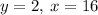
Thus,
(x, y) = (16, 2)
Please note that it seems your answer choices have not included the correct option.