Question

Find the illegal values of b in the fraction 2b^2+3b-10/b^2-2b-8

A. b = -5 and 2
B. b = -2 and 4
C. b = -2 and -4
D. b = -5, -2, 2, and 4

Answer 1

that is the ones that make the denomenator 0

b^2-2b-8=0
solve
factor
(b-4)(b+2)=0
b=4 and -2

answer is B

Answer 2

The correct option is B

Step-by-step explanation:

we have to find the illegal values of b in the fraction

`(2b^2+3b-10)/(b^2-2b-8)`

The values of b that makes the denominator 0 which are illegal values of b in the fraction

`(2b^2+3b-10)/(b^2-2b-8)`

`b^2-2b-8=0`

solve factor

`b^2-2b-8=0`

By middle term splitting method

`b^2-4b+2b-8=0`

`b(b-4)+2(b-4)`

`(b-4)(b+2)`

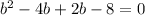
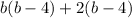
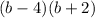
b=4 and -2

The correct option is B