Question

The equation for the circle is:

x^2+y^2−12x+6y−19=0x2+y2−12x+6y−19=0 .
What is the center of the circle?

(-6, 3)
(12, -6)
(6, -3)

(-12, 6)

Answer 1

Hope this helps you.

Answer 2

Option (c) is correct.

Center of circle is at (6, -3)

Explanation:

Given : The equation of circle is
`x^2+y^2-12x+6y-19=0`

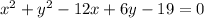
We have to find the center of given circle and choose from the given options.

The standard equation of circle with center (h,k) and radius r is written as

`(x-a)^2+(y-b)^2=r^2`

Consider the given equation
`x^2+y^2-12x+6y-19=0`

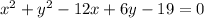
Adding 19 both side, we have,

`x^2-12x+y^2+6y=19`

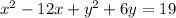
Group x and y terms together, we have,

`\left(x^2-12x\right)+\left(y^2+6y\right)=19`

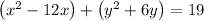
Add both side 36 to make x a perfect square term,

`\left(x^2-12x+36\right)+\left(y^2+6y\right)=19+36`

Using identity
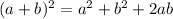`(a+b)^2=a^2+b^2+2ab`, we have,

`\left(x-6\right)^2+\left(y^2+6y\right)=19+36`

Similarly, for y , adding 9 both side,

`\left(x-6\right)^2+\left(y^2+6y+9\right)=19+36+9`

`\left(x-6\right)^2+\left(y+3\right)^2=64`

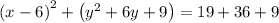
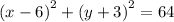
rewriting in standard form , we have,

`\left(x-6\right)^2+\left(y-\left(-3\right)\right)^2=8^2`

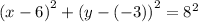
Thus, Center of circle is at (6, -3)

Option (c) is correct.