Answer:
48 km
Explanation:
Let us assume that, the distance of the track where they raced is x km.
We know that,
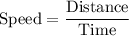
or

Bob runs an average of 12 kilometers per hour. So time taken by Bob is,

Sue runs an average of 8 kilometers per hour. So time taken by Sue is,

Bob finishes 2 hours before Sue, so




 km
km