The distance across the Red River (d) is 1.62 km.
In similar triangles, corresponding sides are proportional. Let's denote the sides of the two triangles as follows:
Triangle 1:
a,b,c (where c is the side across the Red River)
Triangle 2:
A,B,C (where C is the corresponding side in Triangle 2)
Given that the triangles are similar, you can set up the following proportion:
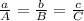
In your case, you mentioned that the sides of Triangle 1 are 0.9 km, 1 km, and d km, and the sides of Triangle 2 are 0.9 km, 1.8 km, and an unknown side (let's call it D km).
Setting up the proportion:
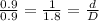
Now, you can solve for d by cross-multiplying:
0.9×1.8=1×d
1.62=d
So, the distance across the Red River (d) is 1.62 km.