Question

The random variable Y is normally distributed with a mean of 470, and the value Y=340 is at the 15th percentile of the distribution. Of the following, which is the best estimate of the standard deviation of the distribution?

A) 125
B) 135
C) 145
D) 155
E) 165

Answer 1

The empirical rule says that about 68% of any normal distribution lies within one standard deviation of the mean. This leaves 32% of the distribution that lies outside this range, with about 16% to either side.

At the 16th percentile, there is a value of
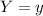
`Y=y` such that


`\mathbb P(Y<y)=\mathbb P\left(\frac{Y-470}\sigma<\frac{y-470}\sigma\right)=\mathbb P(Z<-1)\approx0.16`

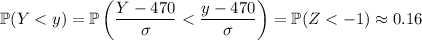
where
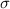
`\sigma` is the standard deviation for the distribution, and
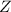
`Z` is the random variable corresponding to the standard normal distribution. This value of
`y` would correspond roughly to a z-score of
`Z=-1`.

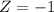
You're told that
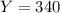
`Y=340` lies at the 15th percentile, so that


`\mathbb P(Y<340)=0.15`

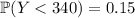
Roughly, then, it'd be fair to say that
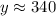
`y\approx340`. So you have


`\frac{340-470}\sigma\approx-1\implies\sigma\approx130`

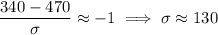
which falls between (A) and (B). To narrow down the choice, notice that
`y` would have be slightly larger than 340 in order to have
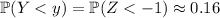
`\mathbb P(Y<y)=\mathbb P(Z<-1)\approx0.16`. This brings
`y` closer to the mean, and thus suggests the standard deviation for the distribution is actually smaller than our approximation.

This tells us that (A) is the answer.