The empirical rule says that about 68% of any normal distribution lies within one standard deviation of the mean. This leaves 32% of the distribution that lies outside this range, with about 16% to either side.
At the 16th percentile, there is a value of
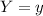
such that
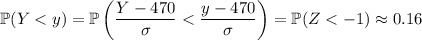
where
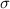
is the standard deviation for the distribution, and
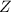
is the random variable corresponding to the standard normal distribution. This value of
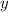
would correspond roughly to a z-score of
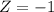
.
You're told that
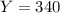
lies at the 15th percentile, so that
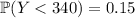
Roughly, then, it'd be fair to say that
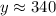
. So you have
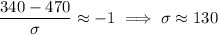
which falls between (A) and (B). To narrow down the choice, notice that
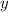
would have be slightly larger than 340 in order to have
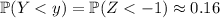
. This brings
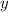
closer to the mean, and thus suggests the standard deviation for the distribution is actually smaller than our approximation.
This tells us that (A) is the answer.