Question

A figure is a cylinder with a radius of 6 inches and a height of 10 inches. On top of the cylinder is a hemisphere with a radius of 6 inches. Find the volume.

A) 102π in3
B) 348π in3
C) 504π in3
D) 888π in3

Answer 1

C, 504
`\pi` in3

Answer 2

C.
`504\pi\text{ inches}^3`

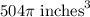
Explanation:

We have been given that a figure is a cylinder with a radius of 6 inches and a height of 10 inches. On top of the cylinder is a hemisphere with a radius of 6 inches.

The volume of our given figure will be equal to volume of cylinder plus volume of hemisphere.

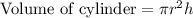`\text{Volume of cylinder}=\pi r^2h`, where,

r = Radius of cylinder,

h = height cylinder.

Upon substituting our given values in above formula we will get,

`\text{Volume of cylinder}=\pi\text{(6 inch)}^2*\text{ 10 inches}`

`\text{Volume of cylinder}=\pi*36\text{ inch}^2*\text{ 10 inches}`

`\text{Volume of cylinder}=360\pi\text{ inch}3`

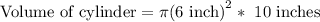
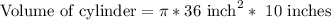
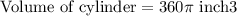
Now let us find the volume oh hemisphere part of our figure using formula,

`\text{Volume of hemisphere}=(2)/(3)\pi r^3`

`\text{Volume of hemisphere}=(2)/(3)\pi*\text{ 6 inches}^3`

`\text{Volume of hemisphere}=(2)/(3)\pi*216\text{ inches}^3`

`\text{Volume of hemisphere}=\pi*2*72\text{ inches}^3`

`\text{Volume of hemisphere}=144\pi\text{ inches}^3`

`\text{Volume of the figure}=\text{Volume of cylinder + Volume of hemisphere}`

`\text{Volume of the figure}=360\pi\text{ inch}3+144\pi\text{ inches}^3`

`\text{Volume of the figure}=504\pi\text{ inches}^3`

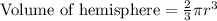
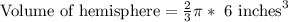
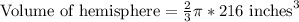
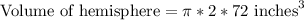
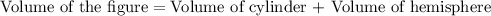
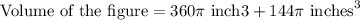
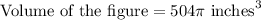
Therefore, the volume of our given figure is
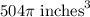`504\pi\text{ inches}^3` and option C is the correct choice.