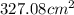Question

Enter the area of a sector with a central angle of 4π/3 radians and a radius of 12.5 cm. Use 3.14 for π and round your final answer to the nearest hundredth.

Answer 1

327.08 cm^2

Explanation:

I just took the test, and I got 100%!

Answer 2

`327.08cm^(2)`

Explanation:

The area of a circular sector is calculated with this expression:

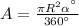`A=(\pi R^(2)\alpha^(\°))/(360\°)}`; where
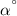`\alpha^(\°)` the central angle, and
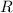`R` is the radius.

Then, we replace all values and solve for A:

`A=(\pi R^(2)\alpha^(\°))/(360\°)}= ((12.5)^(2)((4\pi)/(3)\pi ) )/(360\°)\\A= (2054.1)/(6.28) =327.08cm^(2)`

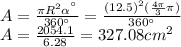
In the problem, we used
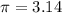`\pi=3.14`, and
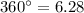`360\°=6.28`, because the problem is asking to use radians, and we cannot operate radians with grades, it would be wrong.

Therefore, the answer is
`327.08cm^(2)`