Answer:
343 : 729
Explanation:
A cube is made up of 6 square faces. If each face has a side length of a, we can find the surface area of that cube with the formula
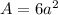 , since we'll have 6 faces with area a². Let's call the edge length of the first cube a and the edge length of the second cube b. The ratio between their surface areas is then 6a² : 6b², or simply a² : b². If we compare this to our given ratio 49 : 81, we can see that a² = 49 and b² = 81, or, square rooting both equations, a = 7 and b = 9.
, since we'll have 6 faces with area a². Let's call the edge length of the first cube a and the edge length of the second cube b. The ratio between their surface areas is then 6a² : 6b², or simply a² : b². If we compare this to our given ratio 49 : 81, we can see that a² = 49 and b² = 81, or, square rooting both equations, a = 7 and b = 9.
The volume of a cube with a side length a is a³, so the ratio between our cubes here must be a³ : b³. Using the values for a and b we just found, this ratio becomes 7³ : 9³, which we can simplify to 343 : 729.