First find any intersection points, set 2 functions equal.
5cos(2x) = 5sin(4x) = 10sin(2x)cos(2x)
5cos(2x)(2sin(2x)-1) = 0
x = pi/4, pi/12
For interval 0 5sin(4x)
For interval pi/12 < x< pi/4, 5sin(4x) > 5 cos(2x)
Set up 2 integrals to express area for each interval.
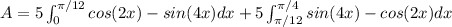
Integrate using u-substitution
![A = 5|_0^(\pi/12) [(1)/(2)sin(2x) +(1)/(4) cos(4x) ] + 5 |_(\pi/12)^(\pi/4) [-(1)/(4)cos(4x) - (1)/(2)sin(2x) ]](https://img.qammunity.org/2018/formulas/mathematics/college/bs43p3ecavun65xf6ehfaukbj12n47rru7.png)
Evaluate limits
![A = 5[((1)/(4) +(1)/(8))-((1)/(4)) ] + 5 [((1)/(4) - (1)/(2))-(-(1)/(8)-(1)/(4)) ] \\ \\ A = (5)/(8) +(5)/(8) = (5)/(4)](https://img.qammunity.org/2018/formulas/mathematics/college/2h1ro76lyau3ncvbccnhbn9056ado1jnhg.png)