Question

Y = 5 cos(2x), y = 5 sin(4x), x = 0, x = π/4
Find its area

Answer 1

First find any intersection points, set 2 functions equal.
5cos(2x) = 5sin(4x) = 10sin(2x)cos(2x)

5cos(2x)(2sin(2x)-1) = 0

x = pi/4, pi/12

For interval 0 5sin(4x)

For interval pi/12 < x< pi/4, 5sin(4x) > 5 cos(2x)

Set up 2 integrals to express area for each interval.


`A = 5\int_0^(\pi/12) cos(2x) - sin(4x) dx + 5 \int_(\pi/12)^(\pi/4) sin(4x) - cos(2x) dx`

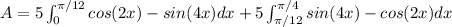
Integrate using u-substitution


`A = 5|_0^(\pi/12) [(1)/(2)sin(2x) +(1)/(4) cos(4x) ] + 5 |_(\pi/12)^(\pi/4) [-(1)/(4)cos(4x) - (1)/(2)sin(2x) ]`

Evaluate limits


`A = 5[((1)/(4) +(1)/(8))-((1)/(4)) ] + 5 [((1)/(4) - (1)/(2))-(-(1)/(8)-(1)/(4)) ] \\ \\ A = (5)/(8) +(5)/(8) = (5)/(4)`