Answer:
hello your question is incomplete attached below is the complete question
answer;
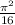
Explanation:
attached below is a detailed solution to the given question above
where :
cos 2x = 1-2sin^2x
cos2x = 2 cos^2x -1
sin^2 2x + cos^2 2x = 1
1-cos^2 2x = sin^2 2x