Question

The standard deviation of a probability distribution table is 26.6 and the mean is 674.0. During an event, you receive the result of 622.3. Determine whether this value is considered usual or unusual and tell why.

A.
Unusual, because the result is less than the minimum usual value.

B.
Usual, because the result is less than the minimum usual value.

C.
Usual, because the result is within the range of the minimum and maximum usual values.

D.
Unusual, because the result is within the range of the minimum and maximum usual values.

Answer 1

The answer would be C. Usual, because the result is within the range of the minimum and maximum usual values.

Answer 2

C. Usual, because the result is within the range of the minimum and maximum usual values.

Explanation:

When the z-scores is lower than -1.96 or higher than 1.96, they are considered as unusual and interesting and they are statistically significant outliers.

The Z score can be calculated by,

`Z=(X-\mu)/(\sigma)`

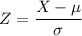
where,

X = raw score = 622.3

μ = mean = 674

σ = standard deviation = 26.6

Putting tall the values,

`Z=(622.3-674)/(26.6)=-1.94`

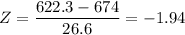
As
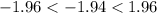`-1.96<-1.94<1.96`, so the result is usual, because it lies within the range of the minimum and maximum usual values.