Answer:
(u o w) (7) = 22
(w o u) 7) = 8
Explanation:
We are given:
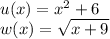
We need to find:
a) (u o w) (7)
First we will find (u o w) (x) and then we will find (u o w) (7)
We know that (u o w) (x) = u(w(x))
Put value of w(x) into u(x)
we have:
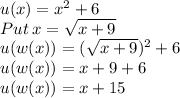
Now finding (u o w) (7)
We know that: (u o w) (7) = u(w(7))
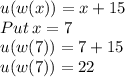
So, (u o w) (7) = 22
b) (w o u) (7)
First we will find (w o u) (x) and then we will find (w o u) (7)
We know that (w o u) (x) = w(u(x))
Put value of u(x) into w(x)
we have:

Now finding (w o u) (7)
We know that (w o u) (7) = w(u(7))

So, (w o u) (7) = 8